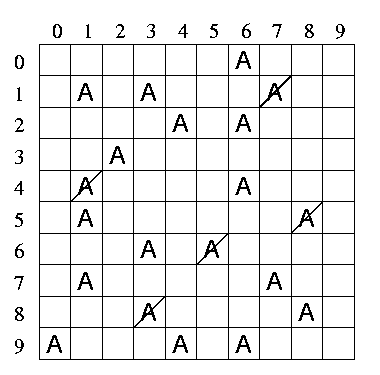
Initially there was 20 mole % of reactant A but some has reacted (crossed out squares).
| Main Contents | Help |
Note: The lecturer will have chosen one of the three manual
experiments for you to do. You do not have to do all three as they
take some time.
The three manual simulations you can do are:
* Manual Simulation of a Monomolecular Reaction in Solution
* Manual Simulation of a Bimolecular Reaction of Two Pure Substances
* Manual Simulation of a Consecutive First Order Reaction
Read the next part which explains how the method works and also read the instructions for the "Manual Simulation of a Monomolecular Reaction in Solution" as that explains the method for the simplest simulation. Then do the manual simulation that the lecturer has suggested.
In the Monte Carlo simulation, the reaction vessel is represented by a grid in which each square is numbered. Figure 1 shows this virtual reaction vessel containing 20 mole % of reactant A (ie. there are 20 molecules marked A in the 100 available positions). The blank squares represent solvent molecules. If we wished to consider the reaction of a pure substance then all positions of the grid would be occupied with reactant A.
 |
Figure 1. Virtual reaction vessel.
Initially there was 20 mole % of reactant A but some has reacted (crossed out squares). |
To perform a Monte Carlo simulation the grid is repeatedly pinpointed in a random fashion by picking a random number. This is callled a "try".When a pinpointed position is occupied by a letter `A' which represents an unreacted molecule the given molecule is considered to have reacted to form molecule `B'. This is represented in Figure 1 by marking off the letters with a cross. If the random selection of a position in the grid hits a crossed-out letter representing a reacted molecule or a vacancy representing a solvent molecule, then such a selection will represent a failed event, or the passage of an element of time without any reaction taking place. The number of letters of A remaining after N tries is equivalent to the concentration [A] and the number of tries N is equivalent to time t. Another way to look at this is that each try is a "tick of the clock".
Now let's consider how we do a Monte Carlo simulation of a bimolecular reaction involving the collision of two reactant molecules A + B ---> C. The progress of such a reaction again depends at any instant upon the probability of a reactive collision taking place. Like the monomolecular reaction we use a grid with the letters A marked on it to represent molecules of type A. This time though we use a second grid of the same size but marked with the letters B to represent molecules of type B. If both reactants are pure substances, that is, not in solution, then all positions on the both grids would be occupied with letters.
This time the procedure is to pick two random numbers for each "try" and pinpoint both grids. A reaction event occurs (ie A + B -> C) if both A and B letters are hit. If only one unreacted molecule is hit or a solvent molecule is hit or a reacted molecule is hit then no reaction takes place.
Materials Supplied
To pinpoint positions in the grid randomly we use a set of uniformly distributed random numbers whose range covers the number of positions in the grid. For a grid of a hundred positions, a set of random digits ranging from 00 to 99 is employed. A printed table of random numbers is provided. An example table, like the printed out one, is shown below.
| Try Number | Random Number | |
|---|---|---|
| 1 | 12 | |
| 2 | 28 | |
| 3 | 36 | |
| 4 | 49 | |
| 5 | 51 | |
| 6 | 65 | |
| 7 | 73 | |
| 8 | 86 | |
| 9 | etc... | |
For each two digit random number take the first digit as the x coordinate and the second digit as the y coordinate for pinpointing the grid. Starting from the top of the table choose the first random number. For subsequent random numbers use the next row down, do not pick random numbers from the table randomly. This can bias the choice towards numbers located near the centre of the table.
So that you don't have too many data points to graph this procedure will use a set of random numbers and we will call this a run. We will then plot the numbers of A remaining after each run. For each run a small set (6 in this case) of random numbers is chosen from the table of random numbers. Pinpoint the appropriate positions on the grid and if an A is hit cross off that position with the marker pen. At the end of each set or run a tally is made of the total number of successful reactions for this run and the remaining number of A's. One run then represents a unit of time and the number of runs N, the elapsed time. The elapsed time simulates the number of attempts of a molecule to decompose in a monomolecular reaction, or for a biomolecular reaction, the number of collisions taking place.
For instance, in the first run you might have picked 23 as the first random number. If a letter A is at site (2,3) cross it off using a pen or pencil. Again pick a random number pair and repeat the procedure another 5 times. After a total of 6 tries we have done one run.
Record your results
Record the remaining number of unreacted molecules A (ie 40 minus
the number that you crossed off) and the time (which will be 1 for the
first run). An example of what your table of results might be like is
shown in the table below.
| Run Number | No. Reacted | No. Remaining |
|---|---|---|
| 0 | 0 | 40 |
| 1 | 4 | 36 |
| 2 | 4 | 32 |
| 3 | 4 | 28 |
| 4 | 3 | 25 |
| 5 | 3 | 22 |
| 6 | 2 | 20 |
| 7 | 1 | 19 |
| 8 | 0 | 19 |
| etc... | ||
Plot results as you go
Plot your results as No. Remaining versus Run Number as you
gather the data. That way you will be able to see when the reaction rate
has effectively slowed and when to stop the simulation.
For the monomolecular reactions, around 100 runs should be sufficient.
Read a pair of two digit numbers from the table, ie two rows. Apply the first number of the pair to one grid for A molecules and the second to the other grid for B molecules. If the first number of the pair selects a molecule A, but the second number applied to the second grid only selects a reacted molecule, then the try is unsuccessful. This represents the occurrence of an unsuccessful collision. If the two tries hit an A and a B then this represents a successfule reaction and we cross off the A and B on both grids. Record your results in a table of Run number, Remaining A and Remaining B.
ln [A] versus N where ln is the natural
logarithm.